Đề cương ôn tập kiểm tra học kỳ II môn Toán Lớp 9 - Năm học 2020-2021 - Trường THCS Lê Hồng Phong

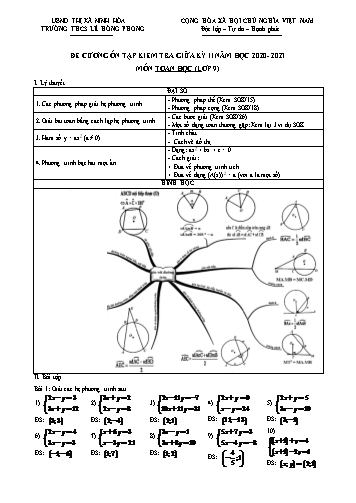
 UBND THỊ XÃ NINH HÒA CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM
 TRƯỜNG THCS LÊ HỒNG PHONG Độc lập – Tự do – Hạnh phúc
 ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA KỲ II NĂM HỌC 2020 - 2021
 MÔN TOÁN HỌC (LỚP 9)
I. Lý thuyết
 ĐẠI SỐ
 - Phương pháp thế (Xem SGK/15)
1. Các phương pháp giải hệ phương trình
 - Phương pháp cộng (Xem SGK/18)
 - Các bước giải (Xem SGK/26)
2. Giải bài toán bằng cách lập hệ phương trình
 - Một số dạng toán thường gặp: Xem lại 3 ví dụ SGK
 - Tính chất
3. Hàm số y = ax2 (a ≠ 0)
 - Cách vẽ đồ thị
 - Dạng: ax2 + bx + c = 0
 - Cách giải:
4. Phương trình bậc hai một ẩn
 + Đưa về phương trình tích
 + Đưa về dạng (A(x))2 = a (với a là một số) 
 HÌNH HỌC
II. Bài tập
Bài 1: Giải các hệ phương trình sau
 2x y 3 3x y 2 2x 11y 7 2x y 9 2x y 5
1) 2) 3) 4) 5) 
 3x y 12 2x y 8 10x 11y 31 x y 24 3x y 10
ĐS: 3;3 ĐS: 2; 4 ĐS: 2;1 ĐS: 11; 13 ĐS: 3; 1 
 2x y 4 x 6y 3 3x y 1 5x 7y 3 10) 
6) 7) 8) 9) 
 3x y 3 x 3y 21 3x 8y 19 5x 4y 8 x 1 y 4
ĐS: 1; 6 ĐS: 1;7 ĐS: 1;2 4 x 1 2y 1
 ĐS: ;1 
 5 ĐS: x; y 2;1 2
3.5. Cho hàm số y = (3m – 2)x2 với m . Tìm điều kiện của m để:
 3
 a) Hàm số đồng biến khi x > 0 b) Hàm số nghịch biến khi x > 0
3.6. Cho hàm số y = (m2 – m + 1)x2. Chứng minh rằng hàm số luôn đồng biến khi x > 0
 1
3.7. Cho hàm số y f x x2 . Không tính hãy so sánh f 99 101 và f 20 .
 2 3
 Gợi ý: Sử dụng tính chất đồng biến, nghịch biến của hàm số.
3.8. Xác định hệ số a của hàm số y = ax2, biết đồ thị của nó đi qua điểm:
 a) M 1; 2 b) M 2; 6 c) M 2;3 
 3
3.9. Xác định hệ số a của hàm số y = ax2 có đồ thị (P), biết đường thẳng y x cắt (P) tại điểm A có 
 2
hoành độ bằng 3.
3.10. Tìm tọa độ giao điểm của parabol (P): y = x2 và đường thẳng (d): y = x + 6. 
 Gợi ý:
 - Cách 1: Dùng đồ thị
 - Cách 2: Dùng phương pháp đại số (Lập phương trình hoành độ giao điểm)
Bài 4: Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn? Xác định các hệ số a, b, 
c và giải phương trình đó
 2
 a) x2 5 b) 3x2 12 0 c) x2 1 2 d) x2 5x x 16
Bài 5: Chứng minh rằng các tứ giác trong các hình vẽ dưới đây nội tiếp được một đường tròn:
 Gợi ý: Sử dụng 4 dấu hiệu nhận biết tứ giác nội tiếp đường tròn (xem SGK/103, mục 15)
Bài 5: Tính số đo các góc trên hình vẽ
a) Tính góc B· DC b) Tính góc B· AC , biết CA = CD. c) Tính góc B· AC , ·ACm
 D
 60
 B
 O
 A C
 m TRƯỜNG THCS LÊ HỒNG PHONG
Họ và tên: 
 ĐỀ CƯƠNG ÔN TẬP KIỂM TRA GIỮA KỲ II NĂM HỌC 2020 - 2021
 MÔN TOÁN HỌC (LỚP 9)
I. Lý thuyết
 ĐẠI SỐ
 - Phương pháp thế (Xem SGK/15)
1. Các phương pháp giải hệ phương trình
 - Phương pháp cộng (Xem SGK/18)
 - Các bước giải (Xem SGK/26)
2. Giải bài toán bằng cách lập hệ phương trình
 - Một số dạng toán thường gặp: Xem lại 3 ví dụ SGK
 - Tính chất
3. Hàm số y = ax2 (a ≠ 0)
 - Cách vẽ đồ thị
 - Dạng: ax2 + bx + c = 0
 - Cách giải:
4. Phương trình bậc hai một ẩn
 + Đưa về phương trình tích
 + Đưa về dạng (A(x))2 = a (với a là một số) 
 HÌNH HỌC
II. Bài tập
Bài 1: Giải các hệ phương trình sau
 2x y 3 3x y 2 2x 11y 7 2x y 9 2x y 5
1) 2) 3) 4) 5) 
 3x y 12 2x y 8 10x 11y 31 x y 24 3x y 10
ĐS: 3;3 ĐS: 2; 4 ĐS: 2;1 ĐS: 11; 13 ĐS: 3; 1 
 2x y 4 x 6y 3 3x y 1 5x 7y 3 10) 
6) 7) 8) 9) 
 3x y 3 x 3y 21 3x 8y 19 5x 4y 8 x 1 y 4
ĐS: 1; 6 ĐS: 1;7 ĐS: 1;2 4 x 1 2y 1
 ĐS: ;1 
 5 ĐS: x; y 2;1 2
3.5. Cho hàm số y = (3m – 2)x2 với m . Tìm điều kiện của m để:
 3
 a) Hàm số đồng biến khi x > 0 b) Hàm số nghịch biến khi x > 0
3.6. Cho hàm số y = (m2 – m + 1)x2. Chứng minh rằng hàm số luôn đồng biến khi x > 0
 1
3.7. Cho hàm số y f x x2 . Không tính hãy so sánh f 99 101 và f 20 .
 2 3
 Gợi ý: Sử dụng tính chất đồng biến, nghịch biến của hàm số.
3.8. Xác định hệ số a của hàm số y = ax2, biết đồ thị của nó đi qua điểm:
 a) M 1; 2 b) M 2; 6 c) M 2;3 
 3
3.9. Xác định hệ số a của hàm số y = ax2 có đồ thị (P), biết đường thẳng y x cắt (P) tại điểm A có 
 2
hoành độ bằng 3.
3.10. Tìm tọa độ giao điểm của parabol (P): y = x2 và đường thẳng (d): y = x + 6. 
 Gợi ý:
 - Cách 1: Dùng đồ thị
 - Cách 2: Dùng phương pháp đại số (Lập phương trình hoành độ giao điểm)
Bài 4: Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn? Xác định các hệ số a, b, 
c và giải phương trình đó
 2
 a) x2 5 b) 3x2 12 0 c) x2 1 2 d) x2 5x x 16
Bài 5: Chứng minh rằng các tứ giác trong các hình vẽ dưới đây nội tiếp được một đường tròn:
 Gợi ý: Sử dụng 4 dấu hiệu nhận biết tứ giác nội tiếp đường tròn (xem SGK/103, mục 15)
Bài 5: Tính số đo các góc trên hình vẽ
a) Tính góc B· DC b) Tính góc B· AC , biết CA = CD. c) Tính góc B· AC , ·ACm
 D
 60
 B
 O
 A C
 m