Giáo án môn Hình học Lớp 10 - Chương trình cả năm - Trường THPT Thị xã Cao Lãnh

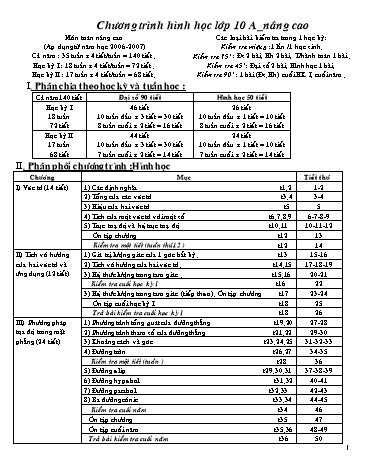
 Chương trình hình học lớp 10 A_nâng cao
 Môn toán nâng cao Các loại bài kiểm tra trong 1 học kỳ:
 (Aùp dụng từ năm học 2006-2007) Kiểm tra miệng :1 lần /1 học sinh.
 Cả năm : 35 tuần x 4 tiết/tuần = 140 tiết . Kiểm tra 15’ : Đs 2 bài, Hh 2 bài. T/hành toán 1 bài .
 Học kỳ I : 18 tuần x 4 tiết/tuần = 72 tiết . Kiểm tra 45’ : Đại số 2 bài, Hình học 1 bài. 
 Học kỳ II : 17 tuần x 4 tiết/tuần = 68 tiết . Kiểm tra 90’ : 1 bài (Đs,Hh) cuối HK I, cuối năm .
 I. Phân chia theo học kỳ và tuần học :
 Cả năm140 tiết Đại số 90 tiết Hình học 50 tiết
 Học kỳ I 46 tiết 26 tiết
 18 tuần 10 tuần đầu x 3 tiết = 30 tiết 10 tuần đầu x 1 tiết = 10 tiết
 72 tiết 8 tuần cuối x 2 tiết = 16 tiết 8 tuần cuối x 2 tiết = 16 tiết
 Học kỳ II 44 tiết 24 tiết
 17 tuần 10 tuần đầu x 3 tiết = 30 tiết 10 tuần đầu x 1 tiết = 10 tiết
 68 tiết 7 tuần cuối x 2 tiết = 14 tiết 7 tuần cuối x 2 tiết = 14 tiết
II. Phân phối chương trình :Hình học
 Chương Mục Tiết thứ
I) Véc tơ (14 tiết) 1) Các định nghĩa t1,2 1-2
 2) Tổng của các véc tơ t3,4 3-4
 3) Hiệu của hai véc tơ t5 5
 4) Tích của một véc tơ với một số t6,7,8,9 6-7-8-9
 5) Trục toạ độ và hệ trục toạ độ t10,11 10-11-12
 Ôn tập chương t12 13
 Kiểm tra một tiết (tuần thứ12 ) t12 14
II) Tích vô hướng 1) Giá trị lượng giác của 1 góc bất kỳ . t13 15-16
của hai véc tơ và 2) Tích vô hướng của hai véc tơ . t14,15 17-18-19
ứng dụng (12 tiết) 3) Hệ thức lượng trong tam giác . t15,16 20-21
 Kiểm tra cuối học kỳ I t16 22
 3) Hệ thức lượng trong tam giác (tiếp theo) . Ôn tập chương t17 23-24
 Ôn tập cuối học kỳ I t18 25
 Trả bài kiểm tra cuối học kỳ I t18 26
III) Phương pháp 1) Phương trình tổng quát của đường thẳng t19,20 27-28
tọa độ trong mặt 2) Phương trình tham số của đường thẳng t21,22 29-30
phẳng (24 tiết) 3) Khoảng cách và góc t23,24,25 31-32-33
 4) Đường tròn t26,27 34-35
 Kiểm tra một tiết (tuần ) t28 36
 5) Đường elíp t29,30,31 37-38-39
 6) Đường hypebol t31,32 40-41
 7) Đường parabol t32,33 42-43
 8) Ba đường côníc t33,34 44-45
 Kiểm tra cuối năm t34 46
 Ôn tập chương t35 47
 Ôn tập cuối năm t35,36 48-49
 Trả bài kiểm tra cuối năm t36 50
 1 Chương 1 Véc tơ
 ******
 Tiết 1-2 §1. CÁC ĐỊNH NGHĨA
I) Mục tiêu :
 - Học sinh nắm được khái niệm véc tơ ( phân biệt được véc tơ với đoạn thẳng ), véc tơ không , 2 véc tơ 
 cùng phương, không cùng phương , cùng hướng, ngược hướng, và hai véc tơ bằng nhau. Chủ yếu 
 nhất là hs biết được khi nào 2 véc tơ bằng nhau . 
II) Đồ dùng dạy học:
 Giáo án, sgk
III) Các hoạt động trên lớp:
 1) Kiểm tra bài củ:
 2) Bài mới:
Tg Nội dung Hoạt động của thầy Hoạt động của trò
 1)Véc tơ là gì ? Gọi hs đọc phần mở đầu của Hs đọc phần mở đầu của sgk
 sgk TL1:
 Câu hỏi 1 : (sgk) Không thể trả lời câu hỏi đó 
 a)Định nghĩa : vì ta không biết tàu thủy 
 Véc tơ là 1 đoạn thẳng có chuyển động theo hướng nào
 hướng, nghĩa là trong 2 điểm mút Gv giới thiệu định nghĩa
 của đoạn thẳng, đã chỉ rõ điểm 
 nào là điểm đầu, điểm nào là điểm 
 cuối ký hiệu 
   
 AB, MN, a , b , x , y  
 b). Véc tơ không :
 Véc tơ có điểm đầu và điểm A B N M
 cuối trùng nhau gọi là véc tơ 
 không . Ký hiệu : 0 Gv giới thiệu véc tơ không : 
   
 3). Hai véc tơ cphương, c/ hướng : AA, BB, 
  
 Với mỗi véctơ AB (khác 0 ), M
 đường thẳng AB được gọi là giá P
  
 của véctơ AB . Còn đối với véc tơ 
  
 –không AA thì mọi đường thẳng 
 đi qua A đều gọi là giá của nó. Q 
 N
 3 HĐ2: Cho hs thực hiện Thực hiện hoạt động2:
 Vẽ đường thẳng d đi qua O và 
 song song hoặc trùng với giá 
 của véctơ a . Trên d xác định được 
 duy nhất 1 điểm A sao cho 
  
 OA= a  và véctơ OA cùng 
 hướng với véctơ a .
3)Củng cố:Véctơ, véctơ-không, 2 véc tơ cùng phương, cùng hướng, bằng nhau 
4)Dặn dò: bt 1,2,3,4,5 trang 8,9 sgk.
 HD:
1) Đoạn thẳng có 2 đầu mút, nhưng thứ tự của 2 đầu mút đó như thế nào cũng được . Đoạn thẳng AB và 
  
 đoạn thẳng BA là một. Véctơ là 1 đoạn thẳng nhưng có phân biệt thứ tự của 2 điểm mút . Vậy AB và 
  
 BA là khác nhau .
2) a)Sai vì véctơ thứ ba có thể là vectơ-không;
 b)Đúng;
 c)Sai vì véctơ thứ ba có thể là vectơ-không;
 d)đúng;
 e)đúng;
 f) Sai.
3)Các véctơ a , d , v , y cùng phương, Các véctơ b , u cùng phương . 
 Các cặp véctơ cùng hứơng a và v , d và y , b và u ;
 Các cặp véctơ bằng nhau a và v , b và u .
4)a) Sai ;b) Đúng; c) Đúng; d)Sai ; e) Đúng; f) Đúng .
    
5)a) Đó là các véctơ BB' ; FO ; CC' .
    
 b) Đó là các véctơ F1F ; ED ; OC .
(O là tâm của lục giác đều ) 
 5 HĐ2: Cho hs thực hiện HĐ2:hs thực hiện hđ2
 A      
 D AB = AC + CB = AD + DB =
   
 O AO + OB
 B
3)Các tchất của phcộng véctơ: C
 HĐ3: Cho hs thực hiện HĐ3:hs thực hiện hđ3:
 b Vẽ hbhành OACB sao cho 
     
 OA = BC = a , OB = AC = b
 C
 A Theo đn tổng của 2 véctơ,ta có 
    
 a a + b = OA + AC = OC ,
    
 b + a = OB + BC = OC .
 O B Vậy a + b = b + a .
 HĐ4: Cho hs thực hiện HĐ4:hs thực hiện hđ4:
 a)Theo đn tổng của 2 véctơ ,
    
 a + b = OA + AB = OB , do đó 
 b B
 A    
 ( a + b )+ c = OB + BC = OC .
 c
 a a+b b)Theo đn tổng của 2 véctơ ,
 b+c
    
 (a+b)+c b + c = AB + BC = AC , do đó 
    
 O
 a+(b+c) C a +( b + c )= OA + AC = OC .
 c)Từ đó có kết luận
 ( a + b )+ c = a +( b + c )
 1) a + b = b + a .
 2) ( a + b )+ c = a +( b + c ) . Chú ý:
 3) a + 0 = a . ( a + b )+ c = a +( b + c )
3)Các qtắc cần nhớ: 
 = a + b + c
*QUY TẮC BA ĐIỂM:
 M
 Với ba điểm bất kỳ M,N,P, 
    
 ta có MN + NP = MP
 P
*QUY TẮC HÌNH BÌNH HÀNH: N
 Với ba điểm bất kỳ M,N,P, 
    
 ta có MN + NP = MP
 7