Một số bài toán đồ thị hay về đồ thị hàm số

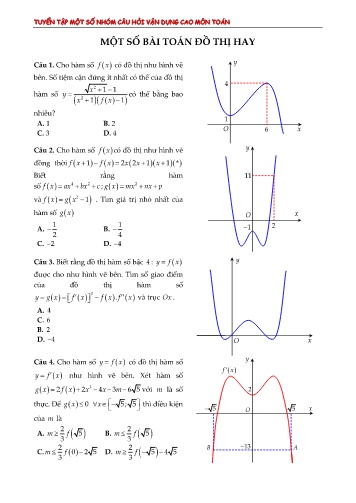
 TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
 MỘT SỐ BÀI TOÁN ĐỒ THỊ HAY 
 Nguyễn Minh Tuấn 
Câu 1. Cho hàm số fx có đồ thị như hình vẽ y
bên. Số tiệm cận đứng ít nhất có thể của đồ thị 
 4
 x2 11
hàm số y có thể bằng bao 
 x2 11 f x 
nhiêu? 
 1
 A. 1 B. 2 
 O 6 x
 C. 3 D. 4 
Câu 2. Cho hàm số fx có đồ thị như hình vẽ y
đồng thời f x 1 f x 2 x 2 x 1 x 1 * 
Biết rằng hàm 11
số f x ax42 bx c ; g x mx2 nx p 
và f x g x2 1 . Tìm giá trị nhỏ nhất của 
hàm số gx O x
 1 1
 A. B. 1 2
 2 4
 C. 2 D. 4 
Câu 3. Biết rằng đồ thị hàm số bậc 4 : y f x y
được cho như hình vẽ bên. Tìm số giao điểm 
của đồ thị hàm số 
 2
y g x f x f x . f x và trục Ox . 
 A. 4 
 C. 6 
 B. 2 
 D. 
 O x
Câu 4. Cho hàm số y f x có đồ thị hàm số y
 fx' 
y f x như hình vẽ bên. Xét hàm số 
g x 2 f x 2 x3 4 x 3 m 6 5 với m là số 2
thực. Để gx 0 x 5; 5 thì điều kiện 
 5 O 5 x
của m là 
 2 2
 A. mf 5 B. mf 5 
 3 3 
 2 2 B 13 A
 C. mf 0 2 5 D. mf 5 4 5 
 3 3
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 1 TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
Câu 9. Cho 0 a 1 b 1 a và hàm số y
 y f x 
 fx 
y g x 2 có đạo hàm trên 
 fx 1 
0; . Biết đồ thị hàm số y f x như n
hình vẽ dưới. Khẳng định nào sau đây đúng 
 m
với mọi x a 1; b 1 
 fb 1 fa 1 
 A. gx B. gx O a b x
 m n
 fb 1 
 C. gx D. 10 gx 0 
 m
Câu 10. Cho hàm số fx có đạo hàm trên y
 \ b và hàm số gx có đạo hàm trên . 
Biết đồ thị của hai hàm số y f x 
y f',' x y g x như hình vẽ dưới. Đặt 
h x f x g x và 
 y g x 
 2
 22 2
S hxb hbx 12 hc hc 
 O a b c x
với a,b,c là các số thực đã biết. Khẳng định 
đúng với mọi x 0 là? 
A. S h c ; h a c B. S h c 
C. S h c ; h a b D. S h a ; h c 
Câu 11. Cho hàm số fx có đạo hàm và x 2
 y
xác định trên tập số thực và có đồ thị như 
hình vẽ dưới. Tính tổng tất cả các giá trị 
nguyên của tham số m  20;20 để hàm 3
số y f x m có 5 điểm cực trị? 
A. 210 
B. 212 3
 O 1 x
C. 211 
D. 209 
 2
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 3 TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
 LỜI GIẢI 
Câu 1. Cho hàm số có đồ thị như hình vẽ 
bên. Số tiệm cận đứngfx ít nhất có thể của đồ thị hàm y
số có thể bằng bao nhiêu? 4
 x2 11
 y 
 A. 1 x2 11 f xB. 2 
 C. 3 D. 4 
 1
 O 6 x 
 Lời giải 
Hàm số có dạng fx y
 21q 
 f x k x2p x x x p q 
 f x1 1 . f . x 211 x 2 x ; 1 6; x 1 1; * 1
 xx22 1 1 1 
 y 11
 42fx 1 2pp2 2qq 122 2 2 2 1
 f x ax bx c g x k . x mx . x nx x11 p . x 1 1 k . x . x x . x 1 1
Trưfờ ng x hợ gp xít2 TCĐ1 nhất là 2pp 2 0 1. khi đó: 
 xx22 1 1 1
 gx y O x
 fx 1 22p 2qq 122 2 1
 1 1 k. x . x x11 . x 1 1 k x x . x 1 1
 1 2
Suy ra2 có TCĐ duy nhất xx4 1 
 2 4
Câu 2. Cho hàm số có đồ thị như hình vẽ 
đồng thời Biết 
rằng hàm số ; 
và . Tìm giá trị nhỏ nhất của hàm 
số 
 A. B. 
 C. D. 
 Lời giải 
Từ * ta thay x 0 f 1 f 0 
 ab 0
Ta có x 0 y 1 c 1 và x 2, y 11 f x x42 x 1 
 c 1
 2
Mặt khác x4 x 2 1 g x 2 1 m x 2 1 n x 2 1 p mx4 2 mx 2 m nx 2 n p 
 m 1 m 1
 1
 21 n n1 gxxxgx 2 ; ' 2 xgx 1; ' 0 x 
 2
 1 np p 0
 1
Vậy giá trị nhỏ nhất gx 
 4
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 5 TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
Câu 4. Cho hàm số có đồ thị hàm số 
 như hình vẽ bên. Xét hàm số 
 với là số thực. 
Để thì điều kiện của là 
 A. B. 
 C. D. 
 Lời giải 
Ta có gx 0 gxfxxxm 2 2436503233 mfxxx 2465 . 
Đặt h x 2 f x 2 x3 4 x 6 5 . Ta có h x 2 f x 6 x2 4 . 
 hf 5 2 5 6.5 4 0
 hf 5 2 5 6.5 4 0
Suy ra hf 0 2 0 0 4 0 
 hf 1 2 1 6.1 4 0
 hf 1 2 1 6.1 4 0
Từ đó ta có bảng biến thiên 
 x 5 0 5 
 h 0 
 h 5 
 h 0 
 h 
 h 5 
 2
Từ bảng biến thiên ta có 35mh mf5 . 
 3 
Câu 5. Cho hàm số fx liên tục và xác y
 y f x y
định trên và có đồ thị fx' như hình vẽ. fx' 
y f x 
Tìm số điểm cực trị của hàm số 
 3
yg x f x22 f x x ? 2 x 4 x 3 m 6 5 m 2
A. 10 gx 0 x 5; 5
 5 O 5 x
B. 11 O
 m 1
C. 12 
 2 2
D. 13mf 5 mf 5 4
 3 3 
 2 2 B 13 A 
 mf 0 2 5 mf 5 4 5
 3 3 Lời giải 
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 7 TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
 0 a 1 blog a 2018 1 1 a 1
Vậy fa loga 2018 1 1 
 fx 2018a
y g x y
Câu 8. Cho hàm2 số bậc ba fx và 
 fx 1 
 2
g x f mx nx p m,, n p có đồ thị như gx fx
0; y f x 
hình dưới, trong đó đường nét liền là đồ thị hàm 2
 fx , đồ thị hàm nét đứt là đồ thị hàm gx , 
 x 1 a 1; b 1
đường x là trục đối xứng hàm . Giá trị 
 2
của biểu thức P n m m p p 2 n bằng bao O 1 2 x
 2 1
nhiêu? 
 2
 A. 6 B. 24 
 C. 12 D. 16 
 Lời giải 
Ta có f x ax3 bx 2 cx d f' x 3 ax 2 2 bx c . Hàm số đạt cực trị tại xx 0; 2 và 
đồ thị đi qua điểm 1;0 , 0;2 nên ta có 
 f ' 0 0 a 1
 f ' 2 0 b 3
 f x x32 32 x 
 f 10 c 0
 f 02 d 2
 32
Ta có g x mx22 nx p 32 mx nx p . Hệ số tự do bằng pp32 32. Đồ thị 
hàm số gx đi qua điểm 0;0 nên p32 3 p 2 0 p 1 . Đồ thị hàm số 
 1
g x f mx2 nx p có trục đối xứng x nên đồ thị hàm số y mx2 nx p cũng có 
 2
 11n
trục đối xứng x m n. 
 2 2m 2
Đồ thị hàm số gx đi qua điểm 2;2 nên 
 mn 1
 32 
 g 2 0 g x 2 m 1 3 2 m 1 2 2 1 
 mn 
 2
Do đồ thị có hướng quay lên trên nên ta suy ra m 01 m n p 
Câu 9. Cho và hàm số có đạo hàm trên 
 . Biết đồ thị hàm số như hình vẽ dưới. Khẳng định nào sau đây đúng với 
mọi 
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 9